Besace (mathématiques)

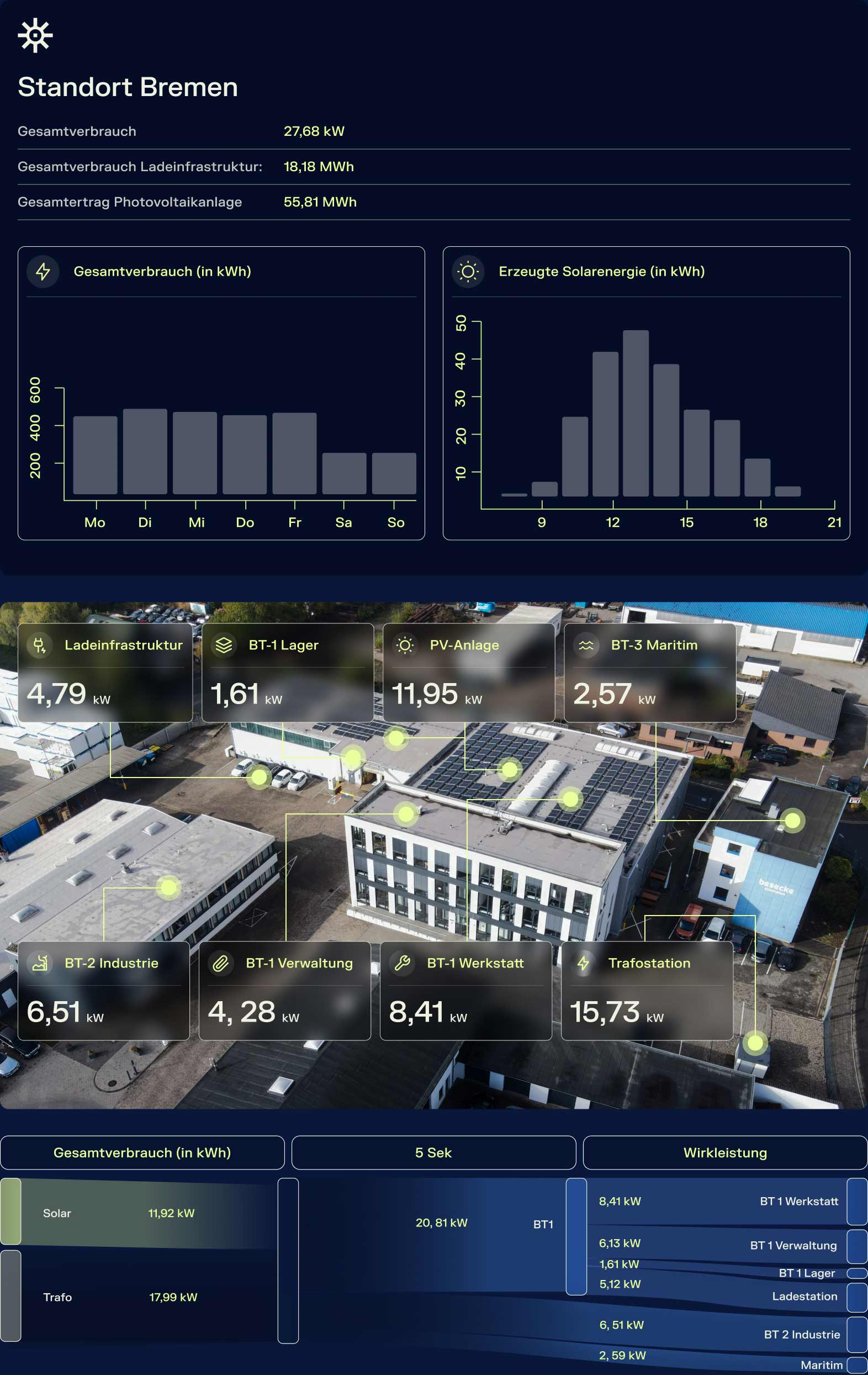
En mathématiques, la besace est une courbe qui a été étudiée et nommée ainsi par Gabriel Cramer en 1750. Son nom évoque une besace, c'est-à-dire un sac ouvert par le milieu et fermé par les deux bouts, en sorte qu’il forme deux poches.

Équations

La besace est une courbe quartique.

Équation cartésienne : ${\displaystyle c^{2}y=bx^{2} ax{\sqrt {c^{2}-x^{2}}}}$ ou ${\displaystyle c^{2}y=bx^{2}-ax{\sqrt {c^{2}-x^{2}}}}$, avec ${\displaystyle c={\sqrt {a^{2} b^{2}}}}$.

Paramétrisation cartésienne : ${\displaystyle {\begin{cases}x=a\cos t-b\sin t\\y=-(\sin t)x\end{cases}}}$, où ${\displaystyle \sin t=-\tan \theta ,t\in [0;2\pi ]}$.

Propriétés

L'aire totale de la besace est ${\displaystyle ac}$.

Les besaces sont les projections de la fenêtre de Viviani sur les plans passant par l’axe du cylindre sur lequel cette fenêtre est découpée.

Ce sont également les projections de la courbe de la crêpe sur les plans passant par l’axe du cylindre associé.

Voir aussi

• Lemniscate de Gerono, un cas particulier de besace

Lien externe

• Besace sur le site mathcurve

• Portail de la géométrie